1.3. Charakterisierung von Netzwerken
Die Distanzmasse, die wir bis jetzt besprochen haben, waren ungehindert in ihrer Ausdehnung und uneingeschränkt in ihrer Richtung. Die meisten Bewegungen im geographischen Raum sind jedoch auf lineare Netze beschränkt, vielfach sind Bewegungen querfeldein nicht möglich. Sogar Flugwege sind begrenzt auf Korridore. Die meisten Bewegungen fliessen entlang von fixen Kanälen: Strassenbahnen (vgl. Abbildung), Pipelines, Telefondrähte, Flusstäler usw. Netzwerke sind für alle Bereiche der Raumwissenschaften von allgemeiner Bedeutung. Vor allem im planerischen Bereich ist die Analyse von Netzwerkstrukturen eine wichtige Aufgabe. So geht es dabei beispielsweise um:
- Optimierung von Netzen: Verbesserung der Verkehrserschliessung durch zusätzliche Strecken im S-Bahnnetz
- Optimale Routenwahl: Planung von Sammeltouren im Abfuhrwesen; Einsatzplanung für Notfalldienste
- Abgrenzen von Einzugsgebieten: Abgrenzung von Feuerwehrkreisen nach Erreichbarkeit im Strassennetz
- Optimale Platzierung im Netz: Angebotszentren (Schulen, Einkaufszentren) im Netz optimal platzieren, d. h. Lokalisierung und Zuteilung von Angebot und Nachfrage.
Eine Vorbedingung für die Analyse solcher Netzwerke ist die analytische Beschreibung und Kenntnis der Netzstrukturen. Dabei geht es im Allgemeinen um die Erreichbarkeit von Objekten. Es lassen sich so Antworten auf folgende Fragen finden:
- Struktureigenschaften eines Netzes: Wie dicht (wie gut verbunden) ist ein Netz?
- Erreichbarkeit von Orten: Wie gut erschlossen ist Ort i im Vergleich zu Ort j (wie oft muss man z. B. umsteigen)?
- Lage im Netz: Welches sind zentrale Orte (d. h. geeignete Umsteigeknoten)?
Der Netzwerkanalyse und -beschreibung liegt die Graphentheorie zugrunde. Damit lassen sich Netze abstrakter und allgemeiner als sogenannte Graphen beschreiben.
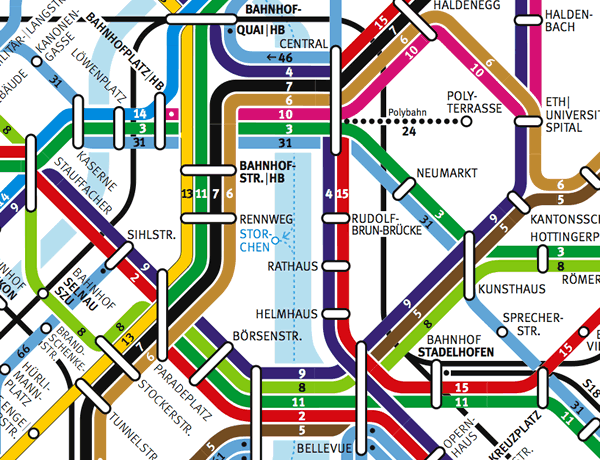Ausschnitt aus dem Netz der Zürcherischen Verkehrsbetriebe; Klicke auf Bild für gesamtes Liniennetz! (VBZ 2006)Lernziele
- Sie kennen die wesentlichen Begriffe, um ein Netz bzw. einen Graphen zu charakterisieren.
- Sie sind in der Lage, einfache Masse zur topologischen und geometrischen Beschreibung von Netzwerken aufzuzählen und zu erklären und können Beispiele für ihre Anwendung geben.
  |
 |
 |