1.3.2. Struktureigenschaften eines Netzes
Konnektivität (Beta-Index)
Das einfachste Mass für den Grad der
Konnektivität (Erschliessungsqualität, Zusammenhang,
Verbundenheit) eines Graphen ist der Beta-Index. Er gibt die Dichte der
Verbindungen an und ist definiert als:  wobei E die Anzahl der Kanten ist und V die Anzahl der Knoten im Graphen.
wobei E die Anzahl der Kanten ist und V die Anzahl der Knoten im Graphen.
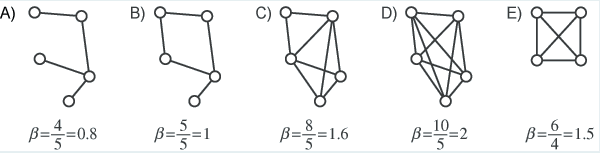 Beta-Index berechnet für verschieden Graphen
Beta-Index berechnet für verschieden GraphenIn der Abbildung oben ist bei den ersten drei Graphen die Anzahl der Knoten konstant gehalten und die Anzahl der Kanten nimmt zu, bis der Graph vollständig ist. Die Werte des Beta-Index nehmen entsprechend zu, je mehr Verbindungen zwischen den Knoten existieren. Die Werte für den Index gehen von 0 aus und sind gegen oben offen, wobei Werte kleiner als 1 auf einen Baum oder auf einen unzusammenhängenden Graphen verweisen. Der Wert 1 zeigt an, dass der Graph nur einen einzigen Zyklus besitzt. Je grösser der Index, desto grösser die Dichte. Damit lassen sich zum Beispiel Bahnnetze verschiedener Regionen oder Länder miteinander vergleichen.
Mit einem solchen Mass lassen sich auch regionale Unterschiede beschreiben. In der nebenstehenden Grafik, wird das Eisenbahnnetz ausgewählter Länder mit der allgemeinen ökonomischen Entwicklung (anhand des Energieverbrauchs-Index in den 60er Jahren) verknüpft. Der Energieverbrauch ist auf der y-Achse geplotted gegenüber dem Mass der Konnektivität (Beta-Index) auf der x-Achse. Dort wo die Konnektivität hoch ist, ist auch die ökonomische Entwicklung weiter fortgeschritten.
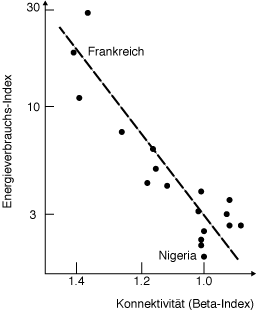 Energieverbrauch gegenüber dem Mass an Konnektivität (Haggett et al. 1977)
Energieverbrauch gegenüber dem Mass an Konnektivität (Haggett et al. 1977)Durchmesser eines Graphen
Ein weiteres Mass für die Struktur eines Graphen ist sein Durchmesser
(engl. diameter). Der Durchmesser Delta ist ein Index, der die topologische
Länge oder Ausdehnung eines Graphen misst, indem die Anzahl der Kanten des
kürzesten Wegs zwischen den am weitesten entfernten Knoten bestimmt wird. Es
gilt 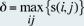 wobei
s(i, j) gleich der kleinsten
Kantendistanz (Kantendistanz = Anzahl der Kanten entlang eines Pfades) zwischen
dem Knoten i und j ist. Die Formel ist so zu verstehen, dass alle kürzesten Wege
zwischen allen Knoten gesucht werden und dann der längste (maximale) ausgewählt
wird. Somit handelt es sich bei diesem Mass um den längsten kürzesten Weg
zwischen zwei beliebigen Knoten eines Graphen.
wobei
s(i, j) gleich der kleinsten
Kantendistanz (Kantendistanz = Anzahl der Kanten entlang eines Pfades) zwischen
dem Knoten i und j ist. Die Formel ist so zu verstehen, dass alle kürzesten Wege
zwischen allen Knoten gesucht werden und dann der längste (maximale) ausgewählt
wird. Somit handelt es sich bei diesem Mass um den längsten kürzesten Weg
zwischen zwei beliebigen Knoten eines Graphen.

Bei den ersten beiden Darstellungen des Graphen A, sind mögliche Pfade eingezeichnet, aber nicht die kürzesten. Im dritten Graph (und auch im Graph B) ist der längste kürzeste Weg eingezeichnet.

Neben der rein topologischen Anwendung kann den Kanten ihre effektive Streckenlänge oder ein anderes Gewicht (z. B. Reisezeit) zugewiesen werden. Daraus lässt sich ein etwas komplexeres und auf der Metrik des Netzes beruhendes Mass bestimmen. Der resultierende Index ist pi = mT/md , wobei mT die metrische Gesamtlänge des Netzes ist und md der metrischen Länge des Durchmessers entspricht. Je grösser pi ist, umso dichter ist ein Netz verbunden.
Erreichbarkeit von Knoten bzw. Orten
Eine häufige Fragestellung bei der Analyse von Verkehrsnetzen ist die
Abklärung der Erreichbarkeit bestimmter Verkehrsknoten und damit der von ihnen
erschlossenen Gebiete. Ein Mass für die Erreichbarkeit (engl. accessibility)
kann durch die in der Animation gezeigte Methode ermittelt werden. Für die
Erreichbarkeit Ei eines Knoten i gilt  wobei v gleich der Anzahl der Knoten im Netz und n(i,
j) gleich der kürzesten Knotendistanz
(Knotendistanz = Anzahl der Knoten entlang eines Pfades) zwischen den Knoten
i und j ist. Es wird also für jeden Knoten i die Summe aller kürzesten Knotendistanzen n(i,
j) zu jedem anderen Knoten gebildet,
was sich am besten mit einer Matrix machen lässt. Die Knotendistanz zwischen
zwei Knoten i und j entspricht der Anzahl dazwischen liegender
Knoten. Für jeden Knoten wird anschliessend die Summe gebildet. Dabei ist die
Erreichbarkeit umso schlechter, je grösser die Summe ist (Knoten A), und umso
besser, je kleiner die Summe ist (Knoten C).
wobei v gleich der Anzahl der Knoten im Netz und n(i,
j) gleich der kürzesten Knotendistanz
(Knotendistanz = Anzahl der Knoten entlang eines Pfades) zwischen den Knoten
i und j ist. Es wird also für jeden Knoten i die Summe aller kürzesten Knotendistanzen n(i,
j) zu jedem anderen Knoten gebildet,
was sich am besten mit einer Matrix machen lässt. Die Knotendistanz zwischen
zwei Knoten i und j entspricht der Anzahl dazwischen liegender
Knoten. Für jeden Knoten wird anschliessend die Summe gebildet. Dabei ist die
Erreichbarkeit umso schlechter, je grösser die Summe ist (Knoten A), und umso
besser, je kleiner die Summe ist (Knoten C).
Die Bedeutung der Knotendistanz liegt darin begründet, dass Knoten auch Umsteigebahnhöfe, Umladeorte für Güter oder U-Bahn-Stationen sein können. Damit behindert eine grosse Knotendistanz die Reise durchs Netz.
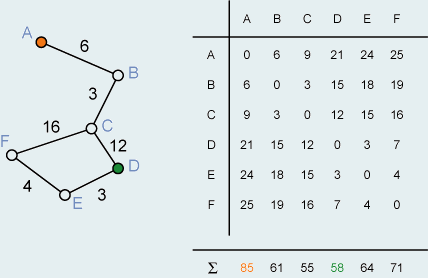 Berechnen der Erreichbarkeit Ei
Berechnen der Erreichbarkeit EiWie schon beim Durchmesser eines Netzes kann neben der rein topologischen
Knotendistanz auch eine gewichtete Kantendistanz verwendet werden. Beispiele für
mögliche Gewichtungsfaktoren sind: die Distanzen in Kilometern oder als
Reisezeit sowie als Transportkosten usw. Für dieses gewichtete Mass wird aber
nicht mehr die Knotendistanz verwendet, sondern die Kantendistanz. Es gilt daher
 wobei e die
Anzahl der Kanten und s(i, j) der
kürzeste gewichtete Pfad zwischen zwei Knoten ist.
wobei e die
Anzahl der Kanten und s(i, j) der
kürzeste gewichtete Pfad zwischen zwei Knoten ist.
Zentralität / Lage im Netz
Das erste Mass für die Beschreibung der Zentralität eines Knotens in
einem Netz wurde von König 1936 entwickelt, die sogenannte KönigszahlKi. s(i, j) bezeichnet die Anzahl der Kanten des kürzesten
Pfades von Knoten i zu Knoten j. Dann ist die Königszahl für den Knoten
i definiert als  wobei s(i, j) gleich der kürzesten Kantendistanz zwischen
den Knoten i und j ist. Somit entspricht Ki dem längsten kürzesten Pfad ausgehend von Knoten i. Es ist ein Mass für die topologische Distanz
mittels Kanten und besagt, je kleiner die Königszahl eines Knotens
i ist, umso zentraler liegt dieser im
Netz.
wobei s(i, j) gleich der kürzesten Kantendistanz zwischen
den Knoten i und j ist. Somit entspricht Ki dem längsten kürzesten Pfad ausgehend von Knoten i. Es ist ein Mass für die topologische Distanz
mittels Kanten und besagt, je kleiner die Königszahl eines Knotens
i ist, umso zentraler liegt dieser im
Netz.
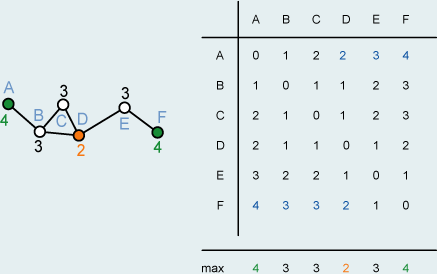
Wenn man die kürzesten Kantendistanzen zwischen den Knoten ermittelt hat,
dann ist der grösste Wert einer Spalte die Königszahl (blau markiert). Im
Beispiel liegt der orange Knoten zentral und die beiden grünen Knoten sind
peripher.
Auch die Methode zur Ermittlung der Königszahl ist anwendbar
auf eine Distanzmatrix. Nebenstehend ist noch einmal das Beispiel der
Erreichbarkeit abgebildet. Diesmal wird die Matrix mit denselben Werten zur
Berechnung der Königszahl verwendet.

Hierarchien in baumartigen Netzen
In der quantitativen Geomorphologie wurden für die Fluvialmorphologie verschiedene Verfahren zur Strukturierung und Ordnung von hierarchischen Flussnetzen entwickelt. So können verschiedene Netze untereinander verglichen werden (z. B. aufgrund der höchsten auftretenden Ordnung oder der relativen Häufigkeiten der einzelnen Ordnungsstufen), und es können auch auf einfache Weise Untereinzugsgebiete ausgeschieden werden. Von den vier Ordnungsschemata in den folgenden Abbildungen sind drei ausschliesslich topologisch definiert, während die Ordnung nach Horton als Einzige auch die metrische Komponente berücksichtigt.
 Strahler-Ordnung Strahler-Ordnung |
Die Strahler-Ordnung wird bestimmt, indem von den äussersten Ästen ausgegangen wird. Diesen äussersten Ästen weist man den Ordnungswert 1 zu. Treffen zwei Äste aufeinander, wird, wenn beide Äste die gleiche Ordnung besitzen, für den weiter unten liegenden Ast die Ordnung um 1 erhöht. Ansonsten wird die höhere Ordnung der beiden Äste eingesetzt. Formal und einfach ausgedrückt:  wobei e1 und e2 die zusammenfliessenden Teilbäume sind und e3 der weiterführende Ast ist. Auf der Basis der Strahler-Ordnung kann die Bifurcation Ratio (Gabelungsverhältnis) ermittelt werden  wobei Ns1 die Anzahl der Kanten einer bestimmten Ordnung (z. B. der Ordnung 1) ist und Ns2 die Anzahl der Kanten der nächsthöheren Ordnung (Ordnung 2) gilt. Im Beispiel der vorliegenden Abbildung ist Ns1 =15 und Ns2 =7, womit sich folgendes Gabelungsverhältnis ergibt:  |
 Horton-Ordnung Horton-Ordnung |
In der Horton-Ordnung wird zunächst eine Ordnung nach Strahler bestimmt. Danach wird dem metrisch längsten Ast der jeweils verbleibenden Teilbäume die noch geltende höchste Ordnung grösser als 2 zugewiesen. |
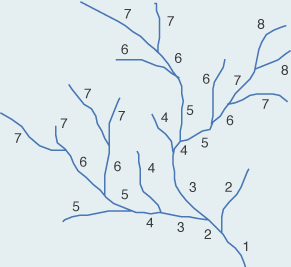
 Shreve-Ordnung Shreve-Ordnung |
Die Shreve-Ordnung (auch Magnitude genannt) eines Teilbaumes gibt an, wie viele Abschnitte erster Ordnung (oder „Quellen“) flussaufwärts liegen. Eine mögliche Anwendung dieser Ordnung ausserhalb der Hydro- oder Geomorphologie liegt in der Wahl von Strichbreiten bei der kartographischen Darstellung von Flussnetzen. |
 Ordnung nach Pfadlänge Ordnung nach Pfadlänge |
Eine einfache Ordnung nach Pfadlänge besteht darin, die Pfadlänge ausgehend von der Wurzel des Baumes zu bestimmen. |
