Thiessen-Polygone

Thiessen-Polygone – auch Voronoi-Polygone oder Voronoi-Diagramme genannt – sind eine wesentliche Methode, um Nähe (Proximität) bzw. Nachbarschaften zu analysieren. Thiessen-Polygone (vgl. Abbildung unten rechts) können verwendet werden, wenn Regionen gesucht sind, die am nächsten zu einem Punkt aus einer Menge von unregelmässig verteilten Punkten liegen. Ein Thiessen-Polygon definiert im zweidimensionalen Fall eine Fläche um einen Punkt, in der jede Raumstelle näher an diesem Punkt liegt als an irgendeinem anderen Punkt. Solche Konstrukte können auch in höheren Dimensionen gebildet werden, wobei dann Thiessen- oder Voronoi-Polyeder entstehen statt Polygone.

Unregelmässig verteilte Punkte oder Stichproben

Punkte mit den dazugehörenden Thiessen-Polygonen

Man kann Voronoi-Diagramme auch um Linien bilden, was dann zu komplexeren Formen führt (siehe untenstehende Abbildung). In dieser Unit beschränken wir uns jedoch auf den einfachsten und am häufigsten verwendeten Fall von Thiessen-Polygonen für Punkte. Eine weiterführende Diskussion bietet (1999).

Rasterzellen Thiessen-Polygone konstruiert um Linienzüge

Da Thiessen-Polygone einem in der Natur (z. B. Zellen von Pflanzen, aneinander stossende Seifenblasen) und in den Raumwissenschaften häufig beobachteten Organisationsprinzip entsprechen, sind die Anwendungsmöglichkeiten mannigfaltig. Zum Beispiel wurden Thiessen-Polygone verwendet, um aus unregelmässig und isolierten Bodenstichproben Bodenkarten zu erstellen. Dabei wurde davon ausgegangen, dass nichts weiter über den Raum zwischen den Stichproben bekannt ist und die Grenzlinie zwischen zwei Stichproben mit unterschiedlichem Bodentyp willkürlich auf halben Weg zwischen ihnen liegt (Beispiel aus (1997, S. 48). Die Thiessen-Polygone können auch verwendet werden, um Einzugsgebiete von Geschäften oder Dienstleistungseinrichtungen abzugrenzen, wenn keine weiteren Informationen zur Verfügung stehen. Eine andere Anwendung ist der Versuch, den Einflussbereich von zentralen Orten zu definieren.

Konstruktion von Thiessen-Polygonen

Wie werden Thiessen-Polygone konstruiert? Die Lösung liegt in ihrer geometrischen Bedeutung begründet. Da Thiessen-Polygone jeweils alle Raumstellen enthalten, die näher beim dazugehörigen Zentrum liegen als bei irgendeinem anderen Zentrum, liegt auf der Hand, dass jede Kante eines Thiessen-Polygons jeweils den geometrischen Ort aller Raumstellen auf dieser bildet, die von zwei Zentren gleich weit entfernt liegen. Weil dem so ist, können die Kanten von Thiessen-Polygonen als Mittelsenkrechte auf die Verbindungslinie d zwischen jeweils zwei Zentren gebildet werden. Mittelsenkrechte konstruiert man durch Schneiden zweier Kreise mit Radius d um die betroffenen Paare von Zentren, wie dies die Abbildung unten zeigt. Die Schnittpunkte der verschiedenen Mittelsenkrechten bilden die Eckpunkte eines Thiessen-Polygons.

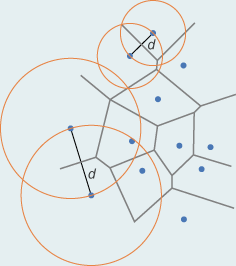Konstruktion von Thiessen-Polygonen (Haggett et al. 1977)

Die Ermittlung von Thiessen-Polygonen im Raster ist übrigens auch möglich. Im Raster kann zwar nicht mehr von Polygonen gesprochen werden, doch ist die Berechnung von Proximitätszonen sehr einfach zu bewerkstelligen. Von einer Anzahl von Punkten aus, gegeben als einzelne Zellen in einem Raster, kann ganz einfach eine Distanztransformation berechnet werden. Die Berechnung im Raster hat den Vorteil, dass auch sehr einfach nicht euklidische Metriken, Gewichtungsfaktoren usw. eingeführt werden können. Mehr zu diesem Thema folgt in der Lektion Erreichbarkeit des Intermediate Levels.

Thiessen-Polygone in einem Raster mit kleiner Auflösung