|
|
Erstellen eines Distanzpuffers
Vektormodell
Die konkrete Lösung für einen Distanzpuffer um eine Linie oder um Polygone besteht nicht einfach in der Bildung paralleler Linien im Abstand l vom Ausgangsobjekt, sondern benötigt in den Stützpunkten zusätzlich Kreisbögen mit dem Radius l. Die Animation zeigt die Konstruktion eines Distanzpuffers um einen Linienzug.
Distanzpuffer um Punkte sind Kreisflächen. Die Punkte in der folgenden Abbildung repräsentieren Standorte von Mobilfunkantennen mit unterschiedlicher Sendeleistung. Dabei ist die äusserste Linie die maximale Reichweite bei gegebener Sendeleistung. Die Distanzpuffer sind hier mit Attributwerten der Ausgangsobjekte gewichtet. Auf der Karte wird ersichtlich, welche Teile der Siedlungsfläche mit einem Empfang abgedeckt sind und welche nicht.
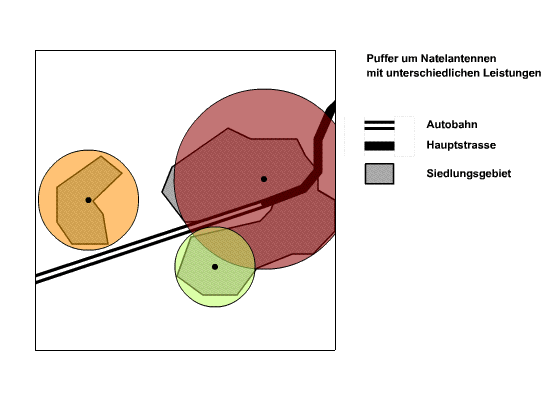 Distanzpuffer um Punkte mit Attributdaten
Distanzpuffer um Punkte mit AttributdatenDie nächsten beiden Beispiele beschäftigen sich mit Distanzpuffern entlang von Linien. Die Linien sind in diesem Fall Strassen unterschiedlicher Klassen. Durch die Einteilung der Strassen ist die Höchstgeschwindigkeit bekannt: Autobahnen 120 km/h und Hauptstrassen 80 km/h. Über ein Immissions-/Emissionsmodell für Strassenlärm (vgl. Lärmorama) wurden die Distanzpuffer für einen Grenzwert von 70 dB abhängig von der erlaubten Höchstgeschwindigkeit berechnet. In das Modell fliessen hauptsächlich drei Parameter ein: durchschnittliche Geschwindigkeit, durchschnittliche Anzahl Fahrzeuge pro Stunden und der Lastwagenanteil. Hindernisse usw. wurden keine berücksichtigt. Es wird davon ausgegangen, dass der Schall sich ungehindert im Raum ausbreiten kann. Die so entstandenen Flächen decken ein Gebiet ab von 85,1 dB an der Verkehrsachse und bis 70 dB an der Umrisslinie des Distanzpuffers (beziehungsweise von 82,9 dB bis 70 dB). Dies bedeutet, dass Pufferfläche nicht homogen ist bezüglich der Beschallung (Immissionswert). Häufig interessiert die Grenzlinie bzw. ein Grenzwert, der mit der Umrisslinie der Pufferfläche markiert ist. Interessant ist diese Fläche aber, wenn z. B. herausgefunden werden möchte, wie gross die Fläche (bzw. Anzahl Einwohner) des Siedlungsgebiets ist, die einem Lärm von 85,1 dB bis 70 dB ausgesetzt ist.
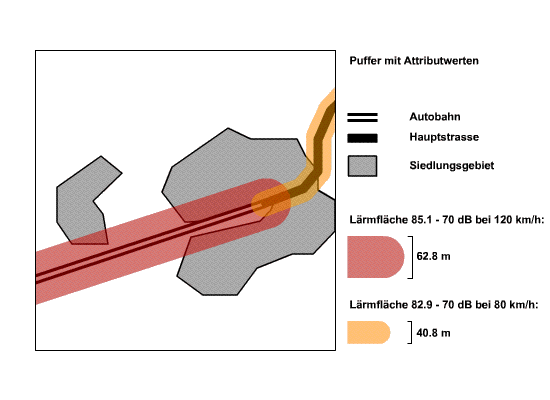 Distanzpuffer um einen Linienzug
Distanzpuffer um einen LinienzugMöchte man eine Abstufung bzw. Verschachtelung der Immissionswerte darstellen, müssen mehrere Distanzpuffer mit den jeweiligen Immissionswerten berechnet werden. Damit die Flächen nicht immer bei 85,1 dB beginnen, müssen sie miteinander verschnitten werden (engl. polygon overlay). Wie Flächen bzw. Polygone verschnitten werden, wird in der Lektion Eignungsanalyse besprochen.
Das letzte Beispiel zeigt einseitige Distanzpuffer, die aufgrund eines Gesetzes festlegt wurden, das bestimmt welche Abstände um ein Naturschutzgebiet für extensive Landwirtschaft (schonender Umgang mit der Natur) und einem allgemeinem Bauverbot gelten.
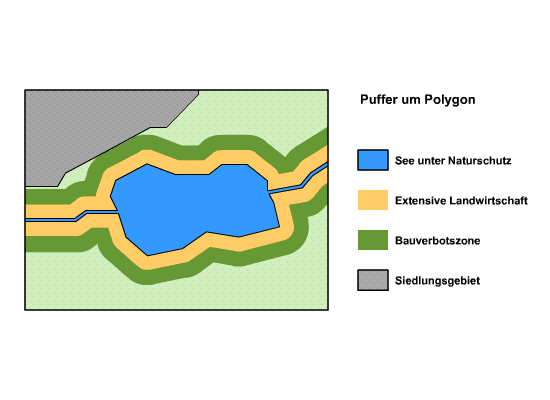 Einseitiger Distanzpuffer um Fläche
Einseitiger Distanzpuffer um FlächeRastermodell
In der Startabbildung der folgenden Animation sind Tramhaltestellen mit dem Zellenwert 7 dargestellt. Ausgehend von diesen beiden „Quellenzellen“ wird nun für jede einzelne Zelle des Rasters die Distanz zur nächstgelegenen Ausgangszelle berechnet. Am Schluss resultiert ein Raster, das aus Distanzen besteht. Die ursprünglichen Haltestellen erhalten somit die Distanz 0. Bei der dargestellten Distanztransformation liegt eine euklidische Metrik zugrunde. Die Werte können in der Animation zu Klassen zusammengefasst werden (engl. reclassify). Ein solcher distanztransformierter Raster könnte beispielsweise als Grundlage dienen, um die von der Distanz abhängigen Immissionswerte des Lärmmodells zuzuweisen. Damit würde eine quasi-kontinuierliche Oberfläche mit Lärmwerten entstehen. Die Genauigkeit und die Kontinuität des Lärmrasters sind nur von der Auflösung des Rasters abhängig. Lärmzonen könnten einfach mit einer neuen Klassierung der Immissionswerte erreicht werden.
In einem Rastermodell ist es auch möglich, eine Distanztransformation für Flächen oder eine beliebige Anordnung von Quellenzellen durchzuführen. Bei der hier dargestellten Zone handelt es sich um Rasterzellen gleicher Thematik, die einen Wald, codiert mit dem Wert 99, darstellen. Für jede Rasterzelle kann man nun den kürzesten Abstand zum Waldrand (gemäss der gewählten Metrik) ermitteln. Die Ergebnisse werden in einem neuen Raster eingetragen. In diesem Raster entsprechen die Werte dem Abstand vom Waldrand. Am Rand des Waldes werden die Werte kleiner sein und werden gegen das Innere des Waldes hoch sein. In unserem Beispiel wurde eine Manhattan-Metrik gewählt. Gemäss dieser Metrik, bei der nur die direkten Nachbarn einer Zelle (4er-Nachbarschaft) berücksichtigt werden, wird diese Region schrittweise jeweils um eine Zellenbreite verdünnt, bis keine Zellen mehr übrig sind. Jeder Verdünnungsschritt wird am Schluss zu einem gemeinsamen Rasterbild addiert. Wie verschiedene Raster kombiniert werden, zeigt die Lektion Eignungsanalyse.
