Metrik

Mit Hilfe einer Metrik können Lage, Richtung und Abstand von Raumobjekten definiert werden. Damit lassen sich beispielsweise Distanzen zwischen Objekten berechnen, kürzeste Wege finden, und es lässt sich der nächste Nachbar identifizieren.
Die euklidische Distanz ist ein Beispiel dafür, was die Mathematik unter einer Metrik versteht. Unter einer Metrik kann einfachheitshalber eine Distanzfunktion verstanden werden. Aus der Schule ist Ihnen der Satz des Pythagoras sicher noch bekannt.

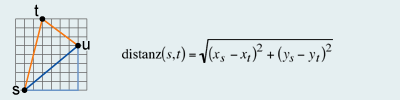Beispiel euklidische Metrik

Damit von einer Metrik im mathematischen Sinne gesprochen werden kann, müssen die unten folgenden drei Bedingungen erfüllt sein.

Metrischer Raum

Ein Menge von Punkten S wird metrischer Raum genannt, wenn eine Funktion distanz() existiert, welche geordnete Paare (s, t) von Elementen aus S zuweist und eine reelle Zahl distanz(s, t) als Wert zurückgibt, der den folgenden drei Bedingungen genügt:

Für jedes Paar s, t in S, distanz(s, t) > 0, wenn s und t disjunkte Punkte sind und
distanz(s, t) = 0, wenn, und nur wenn, s und t identisch sind.
Für jedes Paar s, t in S, ist die Distanz von s zu t gleich wie die Distanz von t zu s;
distanz(s, t) = distanz(t, s).
Für jedes Tripel s, t, u in S ist die Summe der Distanzen von s zu t und von t zu u immer mindestens so gross, wie die Distanz von s zu u, das bedeutet:
distanz(s, t) + distanz(t, u) >= distanz(s, u).
Diese Bedingung ist auch als Dreiecksungleichung bekannt, mit der zusätzlichen Einschränkung, dass die drei Punkte nicht auf einer Geraden liegen.

Die erste Bedingung legt fest, dass die Distanz zwischen zwei Punkten immer eine positive Zahl sein muss, ausser es handelt sich um identische Punkte, womit die Distanz gleich 0 wäre. Die zweite Bedingung stellt sicher, dass die Distanz unabhängig davon ist, in welche Richtung sie gemessen wird. Sie besagt auch, dass die Distanz symmetrisch ist. Die dritte Bedingung bedeutet, dass eine direkte Reise zwischen zwei Punkten maximal so weit ist, wie die Reise über einen dritten Punkt.

Es gibt verschiedene Metriken. Sie finden vor allem in der digitalen Bildverarbeitung Anwendung, wie zum Beispiel in der Fernerkundung. In einem GIS wird vor allem die euklidische Metrik angewendet. Um zu zeigen, welchen Einfluss die gewählte Metrik auf die Distanzberechnung hat, wird die Manhattan-Metrik – auch Cityblock-Metrik oder Taxidriver-Metrik genannt – eingeführt. Gerade an der Karte von Manhattan kann gezeigt werden, dass die Luftlinie in den meisten Fällen nicht geeignet ist, um physisch wirklich überwindbare Distanzen anzugeben. Manhattan ist keine flache, leere Ebene, sondern ist durch sein Strassennetz strukturiert. Die Manhattan-Metrik folgt derselben Logik wie die Fahrt mit einem Taxi in Manhattan: Das Taxi fährt zum Beispiel zwei Blocks nach Norden und anschliessend drei Blocks nach Osten. Es sind also nur Fahrten entlang der vier Haupthimmelsrichtungen möglich, diagonale Fortbewegung durch Häuser ist nicht erlaubt. Formal wird die Manhattan-Metrik wie folgt definiert:

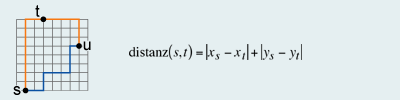Beispiel Manhattan-Metrik

Die Manhattan-Metrik erfüllt alle drei der oben aufgestellten Bedingungen für eine Metrik. Sie ist aber gegenüber der Ausrichtung des Koordinatensystems veränderlich. Werden die Achsen des Koordinatensystems neu orientiert (zum Beispiel um 45 Grad gedreht), dann verändert sich auch die Distanz. Es ist sinnvoll, diese Metrik nur in Städten anzuwenden, die eine rasterähnliche Struktur haben, und die Koordinatenachsen den Strassen folgen zu lassen.
Eine weitere Einschränkung von Metriken für die Distanzberechnung betrifft die Berücksichtigung der Gestalt der Erde. Das Ziel bei der Kartenherstellung ist es, die "Kugelform“ der Erde auf eine Ebene abzubilden. Bei kleinmassstäblichen Karten kann zum Beispiel das geografische Koordinatensystem (Längen und Breiten) in die Ebene abgebildet werden. Das entstandene Koordinatennetz ist aber krummlinig. Für viele Anwendungen und zur Vereinfachung der Berechnungen und Analysen ist es geeigneter, wenn die Karte in einem ebenen kartesischen (rechtwinkligen) Koordinatensystem vorliegt. Dies gilt meistens für Karten mit grossem Massstab (z. B. 1:25'000 bis 1:500'000) wie in der Landeskarte der Schweiz. Bei solchen Karten von Räumen beschränkter Ausdehnung kann die Krümmung der Erdoberfläche vernachlässigt werden. Handelt es sich um Karten mit kleinem Massstab (unter 1:500'000), muss dies jedoch in der Berechnung von Distanzen berücksichtigt werden, das heisst, es muss mit sphärischen Distanzen gerechnet werden.

Einzugsgebiete von Einkaufszentren

Die Karte zeigt die Standorte von vier Warenhäusern. Es ist nicht bekannt, von wo die Kunden stammen. Es wird für eine Analyse Folgendes angenommen: Kunden bevorzugen dasjenige Warenhaus, das am nächsten bei ihrem Wohnort liegt. Zu diesem Zweck wird gemäss der gewählten Metrik die Distanz zwischen zwei benachbarten Warenhäusern halbiert. Die so entstandenen Grenzen weisen den Einkaufszentren ihr Einzugsgebiet zu. Jede Fläche umfasst alle Punkte (Wohnorte), die näher zu dem dazugehörigen Einkaufszentrum liegen. Die so entstandenen Flächen werden Thiessen-Polygone genannt. Wie diese Polygone konstruiert werden, wird in der Unit "Analyse von Distanzbeziehungen“ ersichtlich. Die Animation zeigt, welchen Einfluss die gewählte Metrik auf die Berechnung von Distanzen hat.

Thiessen Polygone mit Manhattan-Metrik und euklidischer Metrik im Vergleich

Zeit als Distanzmass

Ein weiteres Distanzkonzept ist die Wegzeit. Dieses Konzept soll anhand von zwei Karten illustriert werden:

Isochronenkarten (Karten mit Linien gleicher zeitlicher Entfernung)
Zeitkarten (Transformation des geographischen Raumes in einen Zeitraum)

Isochronenkarten:

Die Abbildung zeigt eine Isochronenkarte der Reisezeiten mit der Eisenbahn von London aus für die Jahre 1991 bis 2010 (Spiekermann 1999). Isochronenkarten geben räumlich die zeitlichen Entfernungen aller Punkte die auf einer Karte zu einem bestimmten Ort (z.B. London) wieder. Wo die Isochronen weit auseinander liegen, wird pro Zeiteinheit viel Raumdistanz überwunden bzw. ist das Streckennetz gut ausgebaut, z.B. in Frankreich durch TGV von Lyon nach Paris. Ein Nachteil der Isochronenkarte ist, dass sich zeitliche Entfernungen jeweils nur von einem Ausgangpunkt darstellen lassen und dass die Darstellung der geschichtlichen Entwicklung über mehrere Jahre unübersichtlich wird.

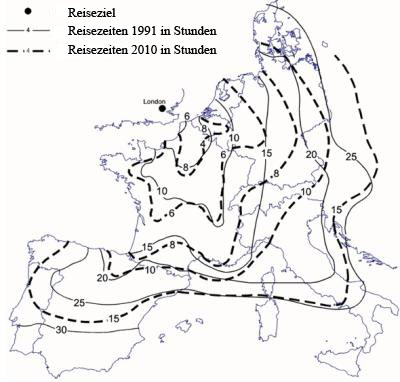Beispiel einer Isochronenkarte (Spiekermann 1999)

Zeitkarten:

Die Abbildung einer Zeitkarte für den Eisenbahnverkehr 1993 stammt wiederum aus (1999). Zeitkarten basieren auf einer mathematischen Methode zu Transformation des euklidischen Raums in den "Zeit-Raum". Schnellere Verkehrsmittel lassen den Raum schrumpfen. Die Orte bewegen sich aufeinander zu. Die Abstände zwischen zwei Punkten auf der Karte sind nicht mehr proportional zur räumlichen Distanz, sondern proportional zu den Reisezeiten zwischen ihnen. Der Kartenmassstab wird also durch Zeiteinheiten gebildet. Die bereits 1993 existierenden TGV-Linien lassen Frankreich schrumpfen, während Südosteuropa relativ dazu wegen der schlechten Schienenverkehrsinfrastruktur aufgebläht wird.

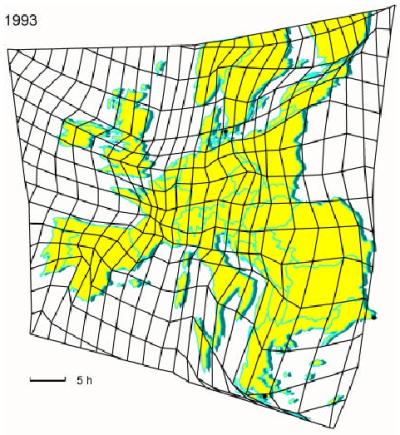Zeitkarte am Beispiel von Reisezeiten (Spiekermann 1999)