|
|
Räumliche Einschränkungen (engl. spatial constraints)
 Eine Strasse kann beispielsweise für kleine Tiere eine räumliche Einschränkung sein. (Photo: Joël Fisler)
Eine Strasse kann beispielsweise für kleine Tiere eine räumliche Einschränkung sein. (Photo: Joël Fisler) Der geographische Raum und der metrische Raum unterscheiden sich in ihren
Eigenschaften wesentlich. Für viele Anwendungen der räumlichen Analyse genügt
der metrische Raum, und Distanzmasse sind die Grundlage vieler Berechnungen. In
der geographischen Raumanalyse sind Beziehungen zwischen Objekten aber nicht nur
durch die reinen metrischen Distanzen bestimmt, die auf dem gegebenen
Koordinatensystem berechnet werden können. Will man die Struktur der im Raum
angeordneten Objekte erklären, sind meist Einschränkungen bzw.
Rahmenbedingungen zu berücksichtigen. Wir gingen bis jetzt stillschweigend davon
aus, dass der Raum zwischen den Objekten homogen und in alle Richtungen gleich
ausgeprägt (also isotrop) ist. Nichts hat die Distanzberechnung beeinflusst
ausser der verwendeten Metrik! Der Raum ist aber in den seltensten Fällen
homogen und isotrop.
Ein Beispiel soll dies verdeutlichen. Die
kürzeste Verbindung in einem Rechteck ist die Diagonale. Möchte man dieses
Rechteck zu Fuss durchqueren, dann wählt man sehr wahrscheinlich diese
Diagonale. Wenn nun dieses Rechteck ein Maisfeld ist, muss mehr Aufwand
geleistet werden, um das Rechteck zu durchqueren, als wenn dieses Feld eine
frisch geschnittene Wiese wäre und es könnte – wenn ein Stier auf der Wiese
steht – sogar sinnvoll sein, dieses Feld zu umgehen. Der Aufwand, der geleistet
wird, um diesen "Reibungswiderstand“ zu überwinden, wird als
Kosten bezeichnet. Dieser Reibungswiderstand wird auch
als Friktion bezeichnet. Steht in einem ausgewählten
Gebiet für jede Raumeinheit der Aufwand für ihre Überwindung zur Verfügung,
spricht man von Kostenoberflächen. Mit solchen
Kostenoberflächen kann man Distanzen gewichten.
 Eisenbahnlinien trennen den Raum und können als räumliche Einschränkung aufgefasst
werden. (Photo: Joël Fisler) Eisenbahnlinien trennen den Raum und können als räumliche Einschränkung aufgefasst
werden. (Photo: Joël Fisler) |
 Für gewisse Menschen stellen auch Check-Points eine räumliche Einschränkung dar. (Photo: Joël
Fisler) Für gewisse Menschen stellen auch Check-Points eine räumliche Einschränkung dar. (Photo: Joël
Fisler) |
Bis jetzt haben wir die Distanzen entlang von Strassennetzen in Manhattan oder aufgrund der Luftlinien betrachtet. Strassennetze können Einbahnstrassen oder Hindernisse wie Barrieren enthalten oder aus verschiedenen Strassenklassen wie Haupt- und Nebenstrassen bestehen, wo unterschiedliche Geschwindigkeitslimiten gelten. Will man den schnellsten Weg zwischen einem Ausgangsort und einem Ziel berechnen, müssen diese Attribute, die den Strassen zugeordnet sind, berücksichtigt werden. Ist man anstelle der schnellsten Flugverbindung von Zürich nach Havanna an der kostengünstigsten Verbindung interessiert, kann es sein, dass ein indirekter Flug zum Beispiel mit Umsteigen in Paris bedeutend günstiger ist. Somit ist die indirekte Verbindung in monetären Einheiten kürzer als die direkte. Oft sind praxis-relevante Distanzen also weder symmetrisch noch macht die Dreiecksungleichung Sinn. Daraus folgt, dass Räume für geographische Fragestellungen nicht nur über eine Metrik definiert werden können und dass es daneben auch nicht-metrische Räume gibt.
Einzugsgebiet von Bahnstationen
Das folgende Beispiel stammt aus Jermann (2002) Eine Bahnlinie bedient eine Ortschaft mit zwei Haltestellen. Buslinien dienen als Zubringer. Dem Liniennetz ist ein Hektarraster unterlegt. Es ist bekannt, wie viele Einwohner und Arbeitsplätze pro Rasterzellen existieren. Man möchte nun wissen, wie gross das Potenzial jeder Haltestelle ist, das heisst, wie viele Menschen potenziell diese Bahnstation benützen. Es ist empirisch in Metern bekannt, wie gross die Anziehungskraft einer solchen Haltestelle ist und dies wird zunächst über die Luftlinie modelliert. Dies ergibt einen Kreis um jede Bahnstation (Abbildung 1). Die Einwohner oder die Arbeitsplätze in den eingefärbten Rasterzellen innerhalb der Kreisfläche sind die potenziellen Kunden. Bei dieser ersten Annäherung wurden noch keine Friktionen (oder Kosten der Distanzüberwindung) berücksichtigt.
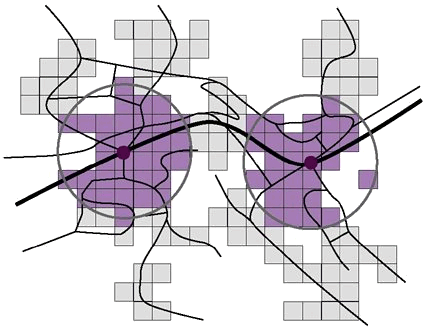 Modellierung des Einzugsbereichs über die Luftdistanz (Jermann 2002)
Modellierung des Einzugsbereichs über die Luftdistanz (Jermann 2002)Das Modell wird in einem zweiten Schritt verfeinert. Hinzu kommt die durchschnittliche Anmarschzeit und ein allgemeiner Umwegfaktor. Das Einzugsgebiet wird nun über eine Zeit definiert. Das Gebiet wird beispielsweise innerhalb einer festgelegten Anmarschzeit zu den Bahnstationen bestimmt. Aus der Literatur ist bekannt, dass die durchschnittliche Fussgängergeschwindigkeit 4,5 km/h beträgt; damit kann der Radius berechnet werden. Anmarschwege weisen gegenüber der Luftlinie einen Umweg auf. Ein gebräuchlicher empirischer Wert für den Umwegfaktor ist 1,25. Damit verkleinert sich der Radius um 20%.
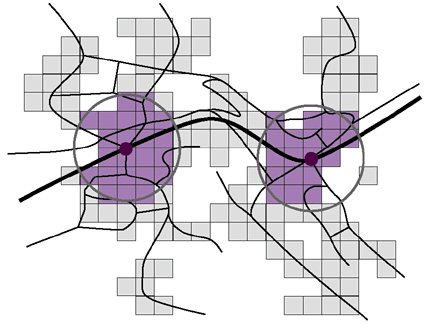 Modellierung des Einzugsbereichs über die Luftdistanz mit Umwegfaktor (Jermann 2002)
Modellierung des Einzugsbereichs über die Luftdistanz mit Umwegfaktor (Jermann 2002)Modelle dieser Art können noch weiter verfeinert werden. Solche Erweiterungen werden von (2002) für Potenzialmodelle des Öffentlichen Verkehrs detailliert diskutiert.
