Zentralität / Lage im Netz

Das erste Mass für die Beschreibung der Zentralität eines Knotens in einem Netz wurde von König 1936 entwickelt, die sogenannte KönigszahlKi. s(i, j) bezeichnet die Anzahl der Kanten des kürzesten Pfades von Knoten i zu Knoten j. Dann ist die Königszahl für den Knoten i definiert als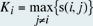
wobei s(i, j) gleich der kürzesten Kantendistanz zwischen den Knoten i und j ist. Somit entspricht Ki dem längsten kürzesten Pfad ausgehend von Knoten i. Es ist ein Mass für die topologische Distanz mittels Kanten und besagt, je kleiner die Königszahl eines Knotens i ist, umso zentraler liegt dieser im Netz.

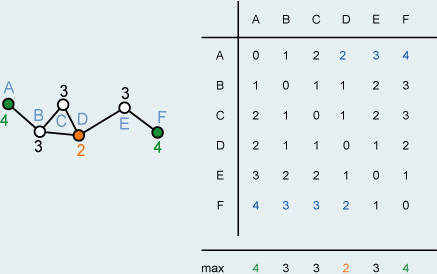
Wenn man die kürzesten Kantendistanzen zwischen den Knoten ermittelt hat, dann ist der grösste Wert einer Spalte die Königszahl (blau markiert). Im Beispiel liegt der orange Knoten zentral und die beiden grünen Knoten sind peripher.
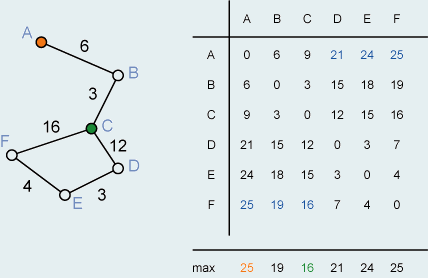
Auch die Methode zur Ermittlung der Königszahl ist anwendbar auf eine Distanzmatrix. Nebenstehend ist noch einmal das Beispiel der Erreichbarkeit abgebildet. Diesmal wird die Matrix mit denselben Werten zur Berechnung der Königszahl verwendet.