|
|
Topologische Beziehungen
Die Topologie beschäftigt sich mit den räumlichen und strukturellen Eigenschaften der geometrischen Objekte unabhängig von ihrer Ausdehnung und ihrer geometrischen Form. Zu den topologischen Eigenschaften gehört die Anzahl Dimensionen eines Objektes und die möglichen Beziehungen zwischen diesen. Alle topologischen Eigenschaften sind invariant bei jeder stetigen Umformung (mathematische Abbildung in sich selbst) des Raumes (Saaty 1980). Die Topologie vereinfacht Analysefunktionen wie die Verfolgung einer Strömung entlang verbundenen Linien eines Netwerkes, das Vereinigen benachbarter Flächen mit ähnlichen Eigenschaften usw. Es ist allerdings zwischen den zwei üblichen Datenformaten zu unterscheiden: Topologische Operationen auf Vektordaten ausgeführt reagieren wesentlich anders als auf Rasterdaten. Man nehme eine Fläche im Vektormodell an. Diese besteht aus einem Rand, der das Innere vom Äusseren der Fläche trennt. Die gleiche Fläche im Rastermodell besteht aus mehreren gleichwertigen Zellen, ein Rand im Sinne einer Trennungslinie ist aber nicht vorhanden. Somit sind die Algorithmen, die für Vektordaten gültig sind, nicht ohne weiteres auf Rasterdaten anwendbar. In der Folge beschränken wir uns auf die topologischen Operationen bei Vektordaten.
VEKTOR Eine interessante Methode zur Klassifikation topologischer Beziehungen wurde von (1993) vorgeschlagen (Worboys et al. 2004). Sie wird als 9-Intersection Schema bezeichnet. Das Intersection-Schema ist ein elegantes Konzept zur Klassifikation von topologischen Konfigurationen. Die grundsätzliche Idee basiert auf dem Konzept, dass jedes Element aus einem Rand (boundary-b), einem Inneren (interior-i) und einem Komplement (exterior-e) besteht. Die Konzepte von Innerem, Rand und Komplement (Äusseres) sind bereits in der allgemeinen Topologie definiert.
Rand
Der Rand besteht aus Punkten oder Linien, welche das Innere vom Äusseren trennen. Der Rand einer Linie besteht aus den Endpunkten. Derjenige eines Polygons ist die Linie, welche den Perimeter definiert.
Inneres
Das Innere besteht aus Punkten, Linien oder Flächen, die im Objekt liegen, aber nicht zum Rand gehören.
Komplement
Das Komplement oder das Äussere besteht aus den Punkten, Linien oder Flächen, die nicht im Objekt sind.
Die grundsätzliche Methode, um zwei Geometrien zu vergleichen, sieht die Untersuchung der Schnittmengen zwischen allen möglichen Paaren vor, welche man mit dem Inneren, dem Äusseren und dem Rand der zwei Geometrien bilden kann. Ausgehend von der resultierenden „Verschnitt“-Matrix kann die Beziehung zwischen den beiden Geometrien klassifiziert werden.
Gegeben sind zwei Objekte A und B mit den jeweiligen erwähnten 3
Komponenten: einen Rand b (boundary), ein Inneres i (interior) und ein Äusseres
e (exterior), so ergeben sich 9 mögliche Beziehungen dazwischen. In der
folgenden Tabelle sind sämtliche topologische Möglichkeiten zwischen zwei
Objekten dargestellt. 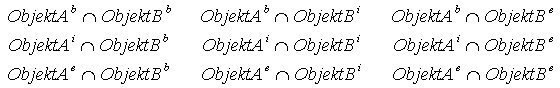
Wenn die dem Komplement entsprechende Zeile und Spalte weglassen werden,
so gelangt man zum 4-Intersection-Schema, welches gelegentlich auch als
Grundlage für die Untersuchung topologischer Beziehungen verwendet wird, aber
nicht so mächtig wie das 9-Intersection-Schema ist. 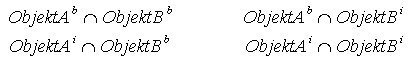
Die wichtigsten topologischen Beziehungen zwischen Objekten, die im GIS-Bereich genutzt werden, sind in der Folge aufgelistet. Dabei ist zu beachten, dass grundsätzlich drei Geometrien vorhanden sind (Punkt, Linie und Fläche), auf welche sich, mit wenigen Ausnahmen, die topologischen Beziehungen anwenden lassen.
Disjunkt (Disjoint)
Objekt A und Objekt B weisen keine Schnittfläche auf. Test auf Getrenntheit (Disjoint) der Ausgangsgeometrie und einer anderen Geometrie.
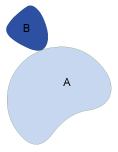
Meet
Objekt A und Objekt B berühren sich an den Grenzlinien. Test auf Berührung (Touch) der Ausgangsgeometrie und einer anderen Geometrie. Die Ränder schneiden sich, nicht aber das Innere der beiden Geometrien. Zwei Geometrien berühren sich, wenn sich nur die Ränder schneiden.
Overlap
Objekt A und Objekt B überschneiden sich.
Test auf Überschneidung (Intersect) der Ausgangsgeometrie und einer anderen
Geometrie (Umkehrung von Disjunkt).
Überlappung mit Getrenntheit: Das Innere
eines Objekts schneidet den Rand und das Innere des anderen Objekts, die beiden
Ränder schneiden sich aber nicht. Das ist der Fall, z. B. wenn eine Linie
ausserhalb eines Polygons (Fläche) beginnt und im Inneren des Polygons endet.
Überlappung mit Überschneidung: Die Ränder
sowie das Innere der beiden Objekte schneiden sich. Wenn eine Geometrie eine
andere schneiden soll, so muss die Geometrie des Schnittes einer kleineren
Dimension in der grösseren vorhanden sein; d. h.:
- Punkte
- Können keine Punkte, Linien oder Flächen schneiden. - Linien
- Könnnen keine Punkte schneiden.
- Können weitere Linien schneiden » Schnitt = Punkte.
- Können Polygonen schneiden » Schnitt = Linien (Punkte).
Contains
Objekt A enthält Objekt B. Test, ob die Ausgangsgeometrie eine andere Geometrie umschliesst (Contains). Das Innere und der Rand eines Objekts sind vollständig im Inneren eines anderen Objekts enthalten. Eine Geometrie kann keine Geometrie höherer Ordnung (Dimension) enthalten; d. h.:
- Punkte können keine Linien oder Fläche enthalten.
- Linien können keine Fläche enthalten.
Inside
Objekt B liegt innerhalb Objekt A. Das Gegenteil zu „enthalten“. Wenn A innerhalb B liegt, so enthält B A.
Covers
Objekt A deckt Objekt B. Das Innere eines Objekts liegt vollständig im Inneren des anderen Objekts, und die Ränder schneiden sich. Eine Geometrie kann keine Geometrie höherer Ordnung (Dimension) enthalten; d. h.:
- Punkte können keine Linien oder Flächen enthalten.
- Linien können keine Fläche enthalten.
Covered by
Objekt B ist von Objekt A bedeckt. Das Gegenteil zu „decken“. Wenn A von B gedeckt ist, so deckt B A.
Equal
Objekt B und Objekt A stimmen überein. Test auf Gleichheit (Equals) der Ausgangsgeometrie und einer anderen Geometrie. Das Innere und der Rand eines Objekts liegen auf dem Rand des zweiten Objekts (und das zweite bedeckt das erste Objekt). Diese Beziehung besteht z. B., wenn eine Linie genau auf den Rand einer Fläche fällt. Die Koordinaten aller einzelnen Bestandpunkte müssen gleich sein. Die verglichenen Geometrien müssen ebenfalls gleich sein; d. h.:
- Punkte = Punkte
- Linien = Linien
- Polygone = Polygone
Die folgende Tabelle zeigt die am häufigsten vorkommenden topologischen Beziehungen:
| poly-poly | line-line | point-point | poly-line | poly-point | line-point | |
|---|---|---|---|---|---|---|
| Disjoint |
 |
 |
|
 |
 |
 |
| Meet |
 |
 |
 |
|
 |
 |
| Overlap |
 |
 |
 |
 |
 |
 |
| Contains |
 |
 |
 |
 |
 |
 |
| Inside |
 |
 |
 |
 |
 |
 |
| Covers |
 |
 |
 |
 |
 |
 |
| Covered by |
 |
 |
 |
 |
 |
 |
| Equal |
 |
 |
|
 |
 |
 |
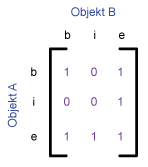
Die folgende Tabelle zeigt das 9-I-Schema und das 4-I-Schma für einige
typische topologische Beziehungen zwischen zwei Flächen, welche von Egenhofer
et al. (1993) vorgeschlagen wurden. Die Beziehungen sind durch die Werte 0 oder 1
gegeben. Jedes Paar hat eine leere (0) oder eine belegte (1) Schnittmenge.
| Topologische Beziehungen | Graphische Darstellung | 4-Intersection-Matrix | 9-Intersection-Matrix |
|---|---|---|---|
| Disjoint |
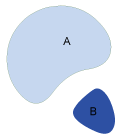 |
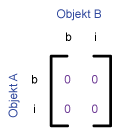 |
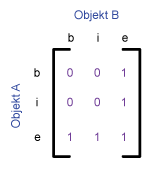 |
| Meet |
 |
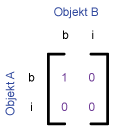 |
 |
| Overlap |
 |
 |
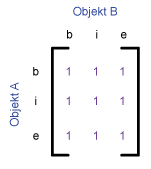 |
| Contains |
 |
 |
 |
| Inside |
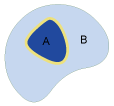 |
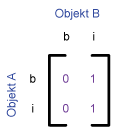 |
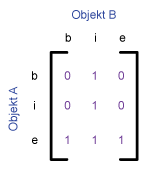 |
| Covers |
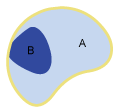 |
 |
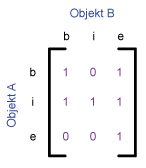 |
| Covered by |
 |
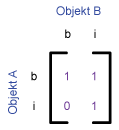 |
 |
| Equal |
 |
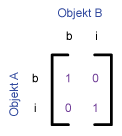 |
 |
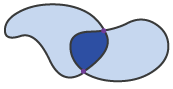
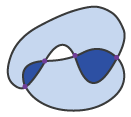
Das gezeigte Modell weist mindestens einen Nachteil auf: Es ist nicht
möglich, konzeptionell unterschiedliche Situationen voneinander zu trennen.
 |
 |
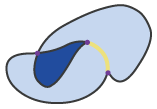 |
Die drei dargestellten Situationen entsprechen der
folgenden Matrix: 
