|
|
Spatial constraints
 Eine Strasse kann beispielsweise für kleine Tiere eine räumliche Einschränkung sein. (Photo: Joël Fisler)
Eine Strasse kann beispielsweise für kleine Tiere eine räumliche Einschränkung sein. (Photo: Joël Fisler)There is a fundamental difference between the geographical space and the metric space. The metric space is adequate
for many applications of spatial analysis, such as distance calculations. In the geographical space, relations
between objects
are not only determined by the metric distance that can be calculated based on the given coordinate system.
In order to explain
the spatial objects, restrictions and conditions have to be considered. Up to now, we assumed space to be
homogeneous and
isotropic.
The distance was determined only by the underlying metric. Nothing has affected the calculation of distance,
except the metric
space. But homogeneous and Isotropic space is rare. Let’s illustrate this with the following example: The
diagonal is the shortest
path in a rectangle, if you want to path from a vertex to its nonconsecutive vertex. If your rectangle is
a corn field, more effort
is required to cross it than in the case it was a freshly cut meadow. Imagine a bull standing on the meadow,
it could be reasonable
to go around it. The effort made to overcome the field (friction) is called cost. The obstacle that has to
be overcame (in this case
the field), is called friction. If, in a given space unit, the cost, that is needed to overcome an obstacle,
is known and displayed,
the surface is called cost surface. Cost surfaces are used for weighting purposes.
 Eisenbahnlinien trennen den Raum und können als räumliche Einschränkung aufgefasst
werden. (Photo: Joël Fisler) Eisenbahnlinien trennen den Raum und können als räumliche Einschränkung aufgefasst
werden. (Photo: Joël Fisler) |
 Für gewisse Menschen stellen auch Check-Points eine räumliche Einschränkung dar. (Photo: Joël
Fisler) Für gewisse Menschen stellen auch Check-Points eine räumliche Einschränkung dar. (Photo: Joël
Fisler) |
Until now we calculated the distances in Manhattan or the Euclidean space. But there can be obstacles on the roads, such as railways, or the road can be composed of different road classes with different speed limits. All these attributes have to be included into the calculation, if you want to calculate fastest route between a starting point and the final destination. In the case that someone is interested to get a cheap flight ticket, e.g. to get from Zürich to Havana, he might take an indirect flight and change plain in Paris. Thus, in a monetary view, the indirect connection is shorter than the direct connection. In practice, distances are in general not symmetric and the triangle inequality doesn’t make sense. Thus, space can't be defined only by metric space.
Catchment area of train stations
The following example was composed by Jermann (2002): In a small town, there are two train stations. Bus lines serve as feeder busses. There is a raster of 1ha cell size underlying the route network. There is a raster layer of 1ha cell size underlying the route network. For each grid cell, the number of inhabitants and the number of employees is given. It is of interest, how many people potentially use those train stations. The drawing power of train stations, expressed in m, is known. It has been detected empirically. This drawing power is modeled based on the beelines, and displayed as circle around the train stations (illustration 1). The residents and the employees within these circles are potential clients of the train stations. The friction (or costs to overcome the distance) was not included in this calculation.
 Modellierung des Einzugsbereichs über die Luftdistanz (Jermann 2002)
Modellierung des Einzugsbereichs über die Luftdistanz (Jermann 2002)The model is improved in a second step. In addition, the average approaching time and a general detour factor are included into the model. This time, the catchment area is specified by the time. The catchment area is defined by a given approach time to the train station. From the literature it is known, that the average pedestrian speed is 4.5km/h. Thus, the radius of the circle can be calculated. Compared to beelines, approach routes exhibit detours. A common empirical value for the detour factor is 1.23. Thus, the radius decreases by 20%.
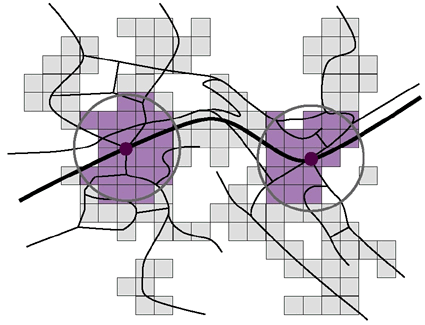 Modellierung des Einzugsbereichs über die Luftdistanz mit Umwegfaktor (Jermann 2002)
Modellierung des Einzugsbereichs über die Luftdistanz mit Umwegfaktor (Jermann 2002)Such models can be further improved. In Jermann (2002) such model extensions for potential models of public transportation are discussed in detail.
