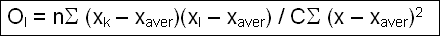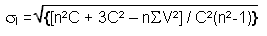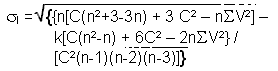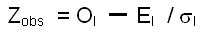Estimate of the number of connections for a random distribution

Whatever the selected null hypothesis (of independence or dependence), the theoretical value for a random distribution, E_I, is calculated the same manner, as presented in Table 2.5 below.

Calculation of the theoretical value EI n: number of zones in the study area Table 2.5

1.2.9a Variability of the theoretical value

With this estimated value EI, is associated a variability expressed by a value of standard deviation σ_I. According to the choice of the null hypothesis, the calculation of σ_I is carried out in the way presented in Table 2.6 below. Once again it is more complex to calculate in the situation of dependency.

Variability of EI for a random theoretical distribution a) According to a null assumption of independence b) According to a null assumption of dependence C: total number of connections between zones V: number of neighbors of each zone n: total number of zones in the study area C: total number of connections between zones V: number of neighbors of each zone n: total number of zones in the study area k: kurtosis of the observed distribution of the values Table 2.6

1.2.9b Calculation of the Moran’s index

The Moran’s index expresses the importance of the difference of properties (values) between all the pairs (x_k, x_l) of contiguous zones

1.2.9c Test of a significant difference between the random and the observed distribution

It is now a question of defining the similarity of the spatial distribution of the properties between the real observed situation and a theoretical random situation. The Z statistic expressing this standardized difference is defined by the equation presented in Table 2.7; it is the same one for the two situations of dependent or independent null hypothesis.

Calculation of z statistic OI: value of Moran’s I index calculated on the observed distribution EI: value of Moran’s I index estimated for a theoretical random spatial distribution σI: standard deviation of the theoretical random distribution a Table 2.7

Once again, two types of test can be applied to question the similarity between the two distributions in a general or specific way, using a bilateral or unilateral test respectively:

• The bilateral test checks to see if the observed spatial distribution of properties in the study area departs from a "random" distribution significantly. the event of rejection of the null hypothesis, one determines that the observed distribution is simply not random. The alternative hypothesis of a bilateral test is, H₁: O_I ≠ E_I .
• The unilateral test checks in a more specific way that the observed spatial distribution of the properties in the study area is significantly closer to either a "grouped" or "dispersed" distribution. Thus one will be able to formulate one of the two following alternative hypotheses, H₁: O_I > E_I or H_1': O_I < E_I . In the event of rejection of the null hypotheses, one deduces that the observed distribution is significantly closer to either a "grouped" distribution, with a strong positive spatial autocorrelation, or to a "dispersed" distribution with a strong negative spatial autocorrelation.