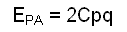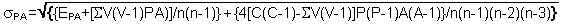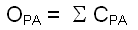Estimate of the number of connections for a random distribution

According to the selected null assumption of independence or dependency, the theoretical number of connections between the areas "presence", P and "absence", A for a random spatial distribution, E _PA, is calculated as described in Table 2.1 below.

Number of connections E PA for a theoretical random spatial distribution a) According to a null hypothesis of independence b) According to a null hypothesis of dependency C: total number of connections between zones p: probability of the property "presence" q: probability of the property "absence" p + q = 1.0 C: total number of connections between zones P: number of zones with the property "presence" A: number of zones with the property "absence" n: total number of zones in the study area n = P + A Table 2.1

1.2.5a Variability of the number of connections for a random distribution

Given a estimated number of connections P/A for a random spatial distribution we can calculate the standard deviation value _σPA. According to the choice of the null hypothesis, the calculation of _σPA can be carried out in the manner presented in Table 2.2 below.

Variability of the number of EPA for a theoretical random spatial distribution a) According to a null hypothesis of independence C: total number of connections between zones V: number of neighbors of each zone ΣV: sum of neighbors of all the zones, with ΣV = 2C p: probability of the property "presence" q: probability of the property "absence" b) According to a null hypothesis of dependency C: total number of connections between zones V: number of neighbors of each zone ΣV: sum of neighbors of all the zones, with ΣV = 2C P: number of zones with the property "presence" A: number of zones with the property "absence" n: total number of zones in the study area Table 2.2

1.2.5b Calculation of the observed join count

The observed join count statistic expresses the total number of connections C between the zones of property "presence" and those of "absence". It can be formulated as followed

1.2.5c Test of a significant difference between the random and the observed distribution

It is now a question of defining the similarity of the spatial distribution of features with "presence" and "absence" between the real observed situation and the theoretically random situation. The use of statistical tests allows us to estimate, with a defined risk of error, if the difference between the number of connections observed O _PA and that of the theoretically and random E _PA is sufficiently large to be regarded as significant. The z statistic, which expresses the standardized difference, is defined by the following equation proposed in Table 2.3. It is the same for the two situations of dependent or independent null hypothesis.

Calculation of z statistic OPA: number of connections P/A between the zones in the area of study EPA: number of connections P/A for a theoretical random distribution σPA: standard deviation of the theoretical random distribution Table 2.3

Two types of test can be applied, answering the question of similarity between the two distributions in a general or specific way, using a bilateral or unilateral test respectively:

• The bilateral test checks if the spatial distribution of zones of "presence" in the study area is significantly different from a "random" distribution. In the event of rejection of the null hypothesis, one determines that the observed distribution is simply random. The alternative assumption of a bilateral test is expressed thus, H ₁: O_PA ≠ E_PA.
• The unilateral test checks in a more specific way if the spatial distribution of the zones of „presence“ in the study area is significantly distributed as either "grouped", or "dispersed". One will be able to thus formulate one of the two following alternative hypothesis, H ₁: O_PA < E_PA or H_1': O_PA > E_PA. In the event of rejection of the null hypothesis, one can determine that the observed distribution will get significantly closer to either a "grouped" distribution, or to a "dispersed" distribution.