|
|
Accessibility (Network Analysis)
The properties of objects along with the relationships between these objects are of interest in spatial analysis. As discussed in the "Spatial Queries" lesson, various relationships between objects can be reviewed. As a basis, thematic (or semantic), spatial or temporal relationships can be detected. Spatial relationships can be further divided into: topological, distance, and directional relationships. In this lesson, the main focus will be on distance relationships. Using methods designed for calculating distances or proximities, one can answer questions such as:
- What is the nearest railway station?
- How many pharmacies are within 300m of a specific location?
- What is the best residential area where the entire route between nursery, school and shopping facilities will be minimal?
- How many residents live in the catchment area of a shopping center?
The measures of distance we have discussed so far were unhindered in their extent and unrestricted in their direction. However, most movements in geographical space are limited to linear networks. In many cases, uninhibited movement is not possible. Even flight paths are limited to corridors. Most movement follows fixed channels: transportation (see figure), pipelines, telephone wires, rivers etc. Networks are of general importance for all areas of spatial science. The analysis of network structures is an important task particularly in the planning area. Network analysis could be about:
- Optimization of networks: improving the transport infrastructure through additional routes in the suburban rail network
- Best route selection: planning trash collecting rounds; resource scheduling for emergency services
- Classification of catchment areas: delineation of fire districts based on accessibility to road network
- Ideal placement in network: optimally positioning supply centers in the network, ie. Locating and allocating for supply and demand
A prerequisite for the analysis of networks is the analytical description and understanding of network structures. Generally, it is about accessibility of objects. You can find answers to questions like:
- Structural properties of a network: how dense (well connected) is a network?
- Accessibility of places: how well connected is place x compared to place y (how often do you need to transfer)?
- Location in the network: what are the central places (i.e. appropriate transfer stations)?
Network analysis and description in based on graph theory. With graph theory, networks can be described in a more abstract and general way as graphs.
Example: For many geographical problems, or even in everyday life, it is not necessary to know exact coordinates (xi, yi). To get from one node to another node in a network, it is most important to know the connections between them. The map (detail) of the London subway system contains all the useful information to get from station i to station j. This topologial representation allows us to see how easy it is to travel between stations that are not adjacent and to find the stops where we need to change.
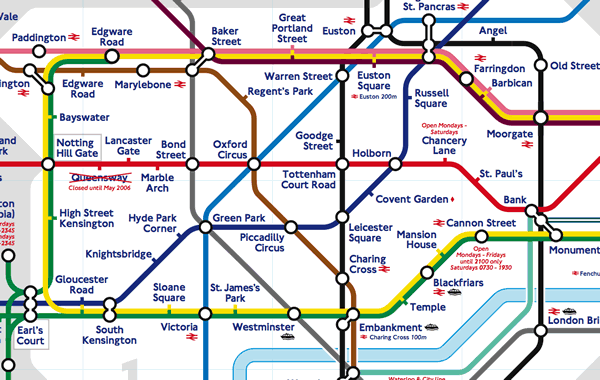 Detail of the map of the London tube. Click on map to see the whole map (Transport for London 2005)
Detail of the map of the London tube. Click on map to see the whole map (Transport for London 2005)Learning Objectives
- You know the essential concepts to characterize a network or a graph
- You are able to list simple measures for topological and geometrical description of networks, to explain them, and to give examples for their application
- You know the most used and famous algorithm, which calculates the shortest path between two points
- You know the problem of the traveling salesman and can explain a heuristic solution
- You can describe the different steps of both algorithms and manually calculate a route for simple cases.
