Surfaces, slopes and aspect

We have just started looking at surfaces, slopes and aspect, but ought to step back a little to impose more order. Many GIS just see elevation as the only important surface -- because they are dimensionally challenged. It is also reasonable to apply reference system criteria to elevation surfaces, measuring them in the same metric. Many applications however also deal with continuous surfaces of other attributes than elevation, but here slope and aspect will not share a metric with the spatial reference system (fall in pH per metre of a profile?).

1. The spatial reference system and surfaces
   • Had GIS incorporated three dimensions, slope and aspect would have been part of the topological system on which attributes were registered. As it is, measurements of attributes, including elevation, are made in the 2D plane, followed by assumptions about the kind of surface they belong to.

   • Often systems simplify surfaces, sometimes treating them as piecewise continuous (a raster DEM), sometimes as continuous with abrupt changes in slopes (TIN -- triangulated irregular network terrain representation), and sometimes for analysis as continuous with continuous rates of change.

   • We will see next week how interpolation lets us estimate the fit of point-based attribute data to fill a study region, and how this may introduce error into the surfaces we use, both for elevation and other attributes of interest.

2. Slope and aspect procedures for DEM
   • In fact most raster GIS provide compound procedures for computing slope and also aspect, the direction in which the slope is facing. The methods used are often refinements of the filter presented above, avoiding for instance problems in determining aspect when slope is close to zero.

   • It is important to remember that filter-based procedures are subject to edge effects, and that they cannot be expected to estimate slope or aspect better than the underlying algorithm. If, as in our example, slope and aspect are taken from fitting a simple plane to 8 points in 2D, the results will not capture significant non-linearity, and may not tackle summits or depressions well.

   • This is partly because a DEM is a 2D piecewise continuous function, and the filters try to force it to be continuous with abrupt changes in slope. The next step logically is to estimate the slope and aspect from draping a continuous function over all the data, and taking derivatives.

   Figure 10: Classified gradients from elevation data using built-in operation.

   

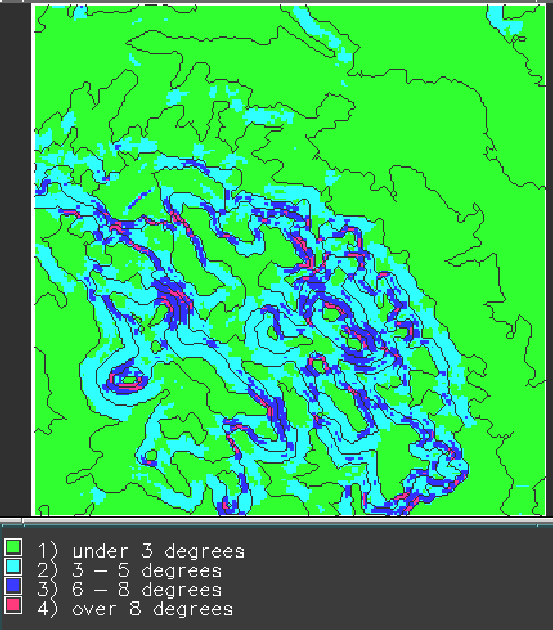   Figure 11: Classified orientation from elevation data using built-in operation.

   

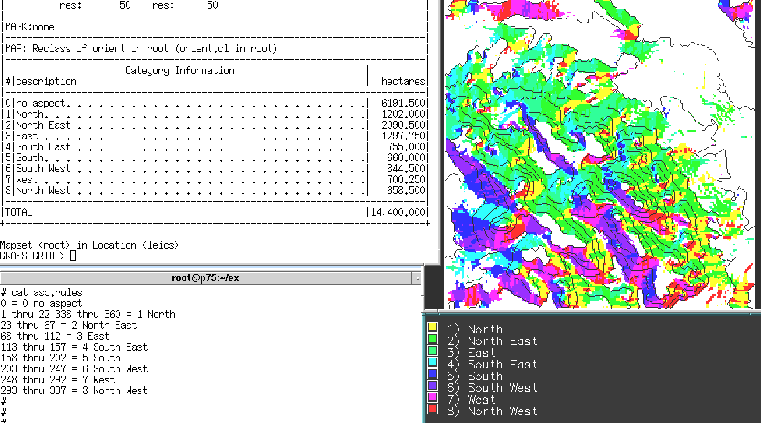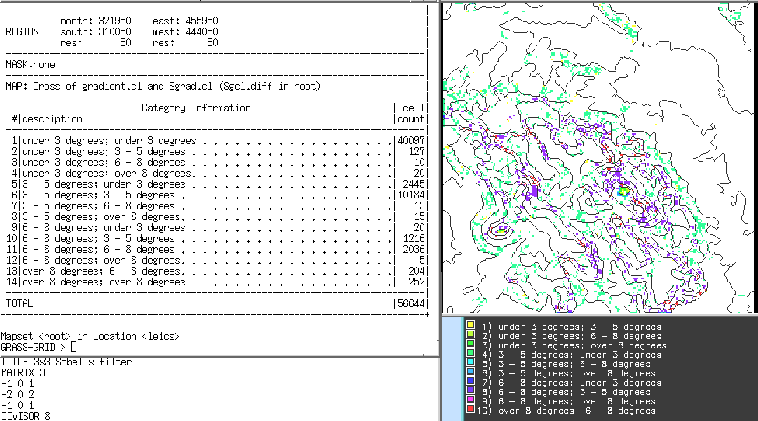
   Figure 12: Differences between classified gradients for built-in and filter-based gradient operations.