Maps of topographic shadows

The determination of topographic shadows is closely related to visibility problems. Just imagine that the viewpoint is located on the sun. Topographic shadow areas are all places without direct solar radiation.
Because the sunrays can be considered parallel, instead of the viewpoint coordinates the suns direction and zenith angle are used. Direction and zenith angle are independent on the location in the DTM. Don’t confuse maps of topographic shadows and shaded relief maps or hillshading.

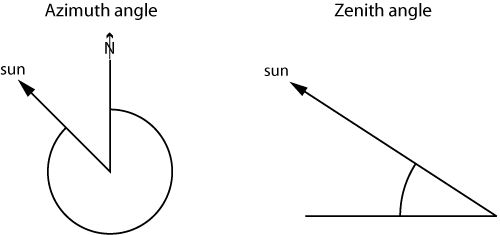Zenith and azimuth angle for indicating the position of the sun.

Topographic shadows can occur due to two effects:

Some slopes of the terrain surface will face away from the incident sunrays and thus be in the shade. This effect is purely local, and the context does not matter. You might use backface culling to extract these areas very quickly.
Shadows can also be cast by the terrain nearby (next figure). This case is more complex since the topographic context must be taken into account.

Shadows can be cast by terrain nearby. Therefore areas may lie in the shade even though they actually face the sun.

If a slope faces the sun the question is, whether the sun lies above or below the horizon. The situation is depicted in the figure below. Thus, a point is in cast shadow if the zenith angle δ to the horizon in the direction of the sun is bigger than the zenith angle of the sun. The zenith angle of the horizon can be calculated using the following formula:

where $Δ z$ is the altitude difference between the horizon and the target point P and d is their distance. If $δ$ is smaller than $γ$ , P lies in the sun, else P lies in the shade. Of course zenith angle $γ$ and direction (azimuth angle) of the sun must be given.

A point P lies in the shade if its zenith angle to the sun (gamma) is smaller than its zenith angle to the horizon (delta).

As you’ve seen, once the horizon at a certain point is known it is relatively straightforward to find out whether a point is in the shade or in the sun. In the case of the analysis of potential direct solar irradiance within a given time period, the position of the sun changes continually. Therefore, cast shadows have to be computed many times for different positions of the sun. Thus, it might be a good idea to extract and store the horizon lines to each grid point in advance and use them in each shadow computation again and again.