|
|
Information derived from a drainage network
An ldd net itself isn’t that useful yet. But given the fact you knew for each raster cell where the water drains to, wouldn’t
it be possible to go the opposite way and count the number of upstream elements for a certain cell? And once you knew the
upstream elements for a certain cell, wouldn’t it be interesting to find out how much water accumulates from all those cells?
An ldd net that has been derived it can be used for a large variety of specific hydrology related analysis. An obvious application
is calculating upstream elements for computing the catchment areas, flow accumulation, ridges or stream channels. Scientists
have proposed many hydrologic indices. Often they aren’t too difficult to calculate with ordinary map algebra software. The
ones discussed here are:
- Wetness index (CTI)
- Stream power index (SPI)
- Sediment transport index (STI)
Upstream elements (Flow Accumulation)
The upstream area is an important factor for the estimation of material fluxes. Given the ldd net Equation 2 makes it quite easy to calculate the number of upstream elements for each raster cell.
Where ci is the ith raster cell with value S(ci) and where SUM(cu) is the sum of all upstream elements draining to ci. Of course these upstream elements can additionally be weighted depending on the actual application. For a flow accumulation
prediction the weights may be set according to the local amount of rain and the share of evaporated, infiltrated and intercepted
water.
In the next illustration top left shows again the ldd net from the figure above. We could then provide an index for each cell
as suggested in the illustration top right and find the upstream elements for each cell (middle left). Applying the equation
shown above with the weights (middle right) results in a upstream elements matrix as shown at the bottom in the illustration.
 Calculating the number of upstream elements for each cell.
Calculating the number of upstream elements for each cell.In the illustration below the upstream elements were calculated for a realistic DEM. The resulting pattern looks quite similar as the river network on an according topographic map.
 Flow accumulations can be computed from an ldd net. (Swisstopo 1991)
Flow accumulations can be computed from an ldd net. (Swisstopo 1991)Stream channels and ridges
By setting a threshold value, it is possible to extract stream
channels from a flow accumulation map. Unlike a flow accumulation map, a map showing stream channels or
ridges merely contains boolean values, i.e. a cell either belongs to a stream channel/ridge or it doesn’t.
You will eventually have to adjust the threshold manually until you get a realistic result. Calculating stream
channels by setting a threshold:
if(upstreamelements >= 50)
then streams=true;
else streams=false;
Computing ridges in a raster can be seen as the dual problem of computing channels. Ridges are by definition
cells with no upstream elements. Brändli (1997) developed and evaluated
various methods for the extraction of geomorphologic and hydrologic features from DTM’s.
Wetness index
The upstream element map can itself be useful for computing other hydrologic indices. A good example is the wetness index (see Beven and Kirkby (1979) in Burrough et al. (1998)) in the next equation, where As is the upstream area (number of upstream elements multiplied by the area of each grid cell) and is the slope at a given cell. The illustration below shows an example of a wetness index map. Obviously the highest values are in channels, the lowest on ridges.
 Wetness index derived from an ldd net. (Swisstopo 1991)
Wetness index derived from an ldd net. (Swisstopo 1991)Stream power index
The stream power index (see Moore et al., 1993 in Burrough et al. (1998)) shown in the following equation is a measure for the erosive power of overland flow. As is the upstream area and is the slope in a given cell. In the following image, you can see that the stream power index map looks quite similar as the map of upstream elements.
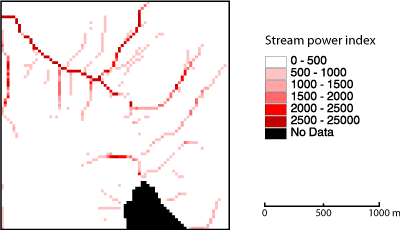 Stream power index derived from an ldd net. (Swisstopo 1991)
Stream power index derived from an ldd net. (Swisstopo 1991)Sediment transport index
The sediment transport index characterises the process of erosion and deposition. Unlike the length-slope factor in the Universal Soil Loss Equation (USLE) it is applicable to three-dimensional surfaces (Burrough et al. 1998). The sediment transport index is defined by the equation below. As is the upstream area and is the slope at a given cell. The next illustration shows an example of a sediment transport index map. The upstream area is weighted stronger than the slope. Therefore the result is not the same.
 Sediment transport index derived from an ldd net. (Swisstopo 1991)
Sediment transport index derived from an ldd net. (Swisstopo 1991)Maximum flow-path length
The maximum flow-path length is the length of the longest flow path from the catchment boundary to a given point in the DEM. Instead of accumulating areas like it is done for upstream areas, it accumulates flow distances across cells, and only the largest flow-path length of all upslope cells is passed on to the down slope cell, instead of the sum (Wilson et al. 2000).
The following illustration displays the maximum flow-path length for a real world example. Obviously hills and ridges have low values, channels have high values continuously increasing downstream.
 Maximum flow-path length in meters to each cell measured upstream. (Swisstopo 1991)
Maximum flow-path length in meters to each cell measured upstream. (Swisstopo 1991)Down slope attributes
The indices described above are all based on the number of upstream elements, which we know how to compute. However, the opposite
problem, i.e. you are asking for downstream elements, is also conceivable. Just imagine you wanted to map proximity to a stream.
How would you find out something like that without adjusting the existing algorithm?
Basically the DEM has to be inverted (next figure) so that peaks become basins and vice versa. This can easily be achieved
by subtracting all DEM values from a value higher than the highest peak in the original DEM. Using the algorithm for extracting
upstream elements, you will get downstream elements which you can use for down slope analyses.
 The original DEM (left) and its inversion (right). (Swisstopo 1991)
The original DEM (left) and its inversion (right). (Swisstopo 1991)