|
|
Kontinuierliche räumliche Variablen
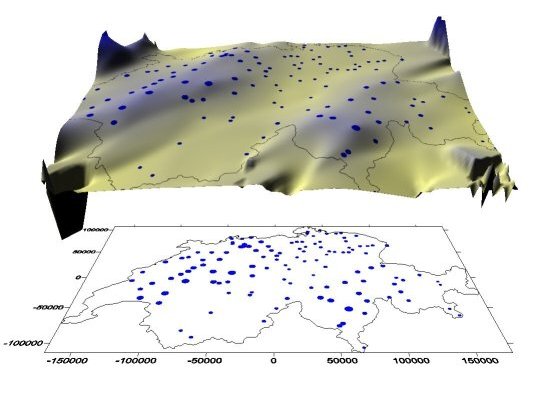 Niederschlagsoberfläche der Schweiz (oben), Karte der Messstationen (unten)
Niederschlagsoberfläche der Schweiz (oben), Karte der Messstationen (unten)Die Abbildung zeigt Ihnen eine Niederschlagsoberfläche der Schweiz: Die blauen Punkte sind die Positionen von Messstationen, ihre Grösse entspricht der Niederschlagsmenge. Die unterschiedlichen Höhen der Oberfläche sowie ihre Farbgebung stehen ebenfalls in Zusammenhang mit der Niederschlagsmenge. Folgende Fragen werden in dieser Lektion behandelt:
- Wie kann aus den ca. 100 Messpunkten solch eine kontinuierliche Oberfläche erstellt werden?
- Welche Werkzeuge helfen uns dabei?
- Welches Wissen ist nötig und welche Methoden existieren dazu?
Was verstehen wir eigentlich unter „Kontinuierlichen Räumlichen Variablen“?
In unserem Eingangsbeispiel ist die Variable der Niederschlag. Führen wir ein Gedankenexperiment durch: Stellen Sie sich vor, Sie könnten den Niederschlag entlang einer Messstrecke auf jeder beliebigen Position messen. Sie hätten also eine räumlich-kontinuierliche Messung. Benachbarte Niederschlagswerte werden entweder identisch sein oder geringfügig variieren, je nach Ihrer Definition der „Nachbarschaft“. Sie dürfen zurecht einwenden, dass ein Niederschlag oft sehr genau definierte Begrenzungen zeigt. Stimmt! Das „Kontinuum Niederschlag“ ist kein mathematisch perfektes. Eventuell gefällt Ihnen die Meereshöhe besser als ein weiteres Beispiel einer kontinuierlichen räumlichen Variablen. Aber praktisch jedes natürliche räumlich-kontinuierliche Phänomen unterliegt gewissen zufälligen Schwankungen. Daher lässt sich auch kaum eines mathematisch perfekt beschreiben (z. B. eine Funktion, die den Anstieg eines Hanges exakt beschriebe, oder die Verteilung unterschiedlicher Boden pH-Werte oder Niederschläge usw.).
Zufalls-Funktion
Aus der Statistik kennen wir deterministische (exakt vorhersehbare und mathematisch beschreibbare) und stochastische (rein zufällige, nicht vorhersehbare) Phänomene. Ein deterministisches Phänomen wäre etwa der Fall eines Gegenstandes: Zu jedem Zeitpunkt können wir exakt vorherberechnen, wo sich der Gegenstand entlang der Falllinie befinden wird. Im Gegensatz dazu denken wir an den Würfelwurf als rein stochastisches Phänomen. In der räumlichen Analyse finden wir Phänomene, die zwischen deterministischen und stochastischen anzusiedeln sind. Sie werden als Zufallsfunktion bezeichnet. Führen wir ein weiteres Gedankenexperiment durch: Betrachten Sie das Beispiel in der folgenden Flash-Animation. Die Punkte stellen Höhenmessungen dar. Die tatsächlichen Höhen zwischen unseren bekannten Messpunkten folgen einer Funktion, die wir jedoch nicht kennen. Wir werden aber davon ausgehen, dass die uns unbekannten Höhen des Profils nicht einfach zufällig verteilt sind, sondern denen der bekannten benachbarten Messpunkte ähneln. Stellen wir also ein Höhenprofil gemäss der blauen strichlierten Linie her. D. h., zwischen die Messpunkte legen wir eine lineare Funktion. Die rote durchgezogene Linie zeigt Ihnen das tatsächliche Höhenprofil. Im letzten Bild sehen Sie die beiden Profillinien im Vergleich. Die Höhe in unserem Beispiel ist solch eine Zufalls-Funktion – weder ist sie exakt mathematisch beschreibbar, noch ist sie rein zufällig!
Bleibt darauf hinzuweisen, dass kontinuierliche räumliche Variablen sich in der Regel besser im Rastermodell abbilden lassen, wenngleich die Rastereinteilung eigentlich wiederum diskrete räumliche Einheiten bildet.
Lernziele
- Sie können die wichtigsten Typen räumlicher Stichprobenziehung beschreiben.
- Sie können Angaben zur sinnvollen Grösse räumlicher Stichprobenziehungen machen.
- Sie beherrschen die Grundlagen der explorativen Variographie.
- Sie können darlegen, weshalb das Wissen um räumliche Abhängigkeiten für die Analyse kontinuierlicher Variablen von Bedeutung ist.
- Sie kennen die wichtigsten Grundlagen räumlicher Schätzverfahren (Interpolationen).
- Sie können sinnvolle Anwendungsbeispiele für Interpolationen nennen.
